如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化.
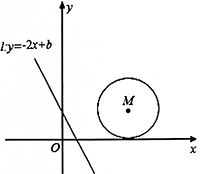
(1)已知⊙M的圆心坐标为(4,2),半径为2.
当b=______时,直线l:y=-2x+b(b≥0)经过圆心M;
当b=______时,直线l:y=-2x+b(b≥0)与⊙M相切;
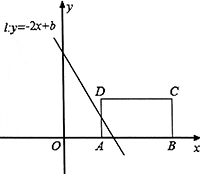
(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.
如图,在平面直角坐标系中,直线l:y=-2x+b(b≥0)的位置随b的不同取值而变化.
(1)已知⊙M的圆心坐标为(4,2),半径为2.
当b=______时,直线l:y=-2x+b(b≥0)经过圆心M;
当b=______时,直线l:y=-2x+b(b≥0)与⊙M相切;
(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.


(1)①直线l:y=-2x+b(b≥0)经过圆心M(4,2)时,则有:2=-2×4+b,∴b=10;②若直线l:y=-2x+b(b≥0)与⊙M相切,如图所示,应有两条符合条件的切线. 设直线与x轴、y轴交于A、B点,则A(b/2,0)、B(0,b),∴OB=2OA.由题意,可知⊙M与x轴相切,设切点为D,连接MD;设直线与⊙M的一个切点为P,连接MP并延长交x轴于点G;过P点作PN⊥MD于点N,PH⊥x轴于点H.易证△PNN∽△BAO,∴PN:MN=OB:0A=2:1,∴PN=2MN.在Rt△PMN中,由勾股定理得:PM2=PN2+MN2,解得:MN=(2)/5,PN=(4)/5,∴PH=ND=MD-MN=2-(2)/5,OH=OD-HD=OD-PN=4-(4)/5,代入直线解析式求得:b=10-2;同理,当切线位于另外一侧时,可求得:b=10+2.(2) 由题意,可知矩形ABCD顶点D的坐标为(2,2).由一次函数的性质可知,当b由小到大变化时,直线l:2x+b(b≥0)向右平移,依次扫过矩形ABCD的不同部分.可得当直线经过A(2,0)时,b=4;当直线经过D(2,2)时,b=6;当直线经过B(6,0...
查看完整答案若一次函数y=2x+2的图象经过点(3,m),则m=_________.
甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算.走得最快的是【 】
在同一平面直角坐标系中,一次函数y=ax+a2与y=a2x+a的图像可能是【 】
已知函数y=ax+b经过(1,3),(0,-2),则a - b=【 】
把函数y=x向上平移3个单位,下列在该平移后的直线上的点是【 】
若一次函数y=x+b(b是常数)的图像经过第一、二、三象限,则b的值可以是______(写出一个即可).
在平面直角坐标系xOy中,一次函数y=kx+b(k>0)的图像与x轴、y轴分别交于A,B两点,且与反比例函数y=4/x的图像的一个交点为P(1,m).(1)求m的值;(2)若PA=2AB,求k的值.
某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是【 】
如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是【 】
在平面直角坐标系中,点P(- 20,a) 与点Q(b,13) 关于原点对称,则a+b的值为【 】
如图所示,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为_________.
如图,在平面直角坐标系中,ΔOAB的顶点A,B的坐标分别为(3,),(4,0).把ΔOAB沿x轴向右平移得到ΔCDE,如果点D的坐标为(6,),则点E的坐标为_________.
在半面直角坐标系中,点(3,2)关于x轴对称的点的坐标为【 】
如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是【 】