竞赛2024年中国数学奥林匹克( )
已知a1,a2,⋯,an为实数,且∑i=1nai =n,∑i=1nai² =2n,∑i=1nai³ =3n.
(1)求最大的常数C,使得对所有n≥3,均有max{a1,a2,⋯,an }-min{a1,a2,⋯,an }≥C;
(2)证明存在常数C2>0使得max{a1,a2,⋯,an }-min{a1,a2,⋯,an }+C≥C2n-3,其中C为(1)中的常数.
竞赛2024年中国数学奥林匹克( )
设p为给定素数,f为{0,1,…,p-1}到自身的一个双射.若f满足:当p|a²-b²时,|f(a)-f(b)|≤2024.求证:有无穷多个p使得f存在,也有无穷多个p使得f不存在.
竞赛2024年中国数学奥林匹克( )
对于R²中任意两点(x1,y1 ),(x2,y2),定义该两点之间的小数距离为:
√(‖x1-x2 ‖²+‖y1-y2 ‖² )
其中‖x‖表示实数x离最近整数的距离.求最大的实数r,使得平面上存在四个点,两两之间的小数距离均不小于r.
解答提示见word版
竞赛2024年中国数学奥林匹克( )
给定整数a1>a2>⋯>an>1,记M=lcm(a1,a2,⋯,an ),对任意非空有限正整数集X,定义
f(X)=min1≤i<n∑x∈X{x/ai }
若对X的任意真子集Y,有f(Y)<f(X),则称X是极小的.设X是极小的,且f(X)≥2/an .
求证:|X|≤f(X)∙M.
解答过程见word版
竞赛2024年中国数学奥林匹克( )
在△ABC中,I为内心,L,M,N分别为,AI,AC,CI的中点,D在线段AM上,满足BC=BD,△ABD的内切圆切边AD,BD于E,F,J为△AIC的外心,ω为△JMD的外接圆,MN再次交ω于P,JL再次交ω于Q,证明:PQ,LN,EF三线交于一点.
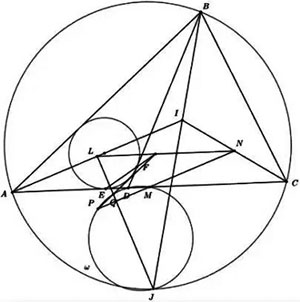
解答过程见word版

