如图,在平面直角坐标系xOy中,直线l:y=1/2 x+4分别与x轴,y轴相交于A,B两点,点P(x,y)为直线l在第二象限的点.
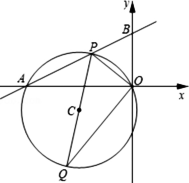
(1) 求A,B两点的坐标;
(2) 设△PAO的面积为S,求S关于x的解析式,并写出x的取值范围;
(3) 作△PAO的外接圆⨀C,延长PC交⨀C于点Q,当△POQ的面积最小时,求⨀C的半径.
如图,在平面直角坐标系xOy中,直线l:y=1/2 x+4分别与x轴,y轴相交于A,B两点,点P(x,y)为直线l在第二象限的点.

(1) 求A,B两点的坐标;
(2) 设△PAO的面积为S,求S关于x的解析式,并写出x的取值范围;
(3) 作△PAO的外接圆⨀C,延长PC交⨀C于点Q,当△POQ的面积最小时,求⨀C的半径.
(1)∵直线l:y=1/2 x+4分别与x轴,y轴相交于A,B两点,∴当x=0时,y=4;当y=0时,x=-8,∴A(-8,0),B(0,4);(2)∵点P(x,y)为直线l在第二象限的点,∴P(x,1/2 x+4),∴S△APO=1/2×OA×(1/2 x+4)=2x+16 (-8<x<0)即 S=2x+16 (-8<x<0);(3)∵A(-8,0),B(0,4),∴OA=8,OB=4,AB==4√5.在⨀C中,PQ是直径,∴∠POQ=90°,∵∠P...
查看完整答案