如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).
(1) m为何值时,△OAB面积最大? 最大值是多少?
(2)如图2,在(1)的条件下,函数y=k/x(k>0)的图像与直线AB相交于C,D两点,若S△OCA=1/8 S△OCD,求k的值.
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).
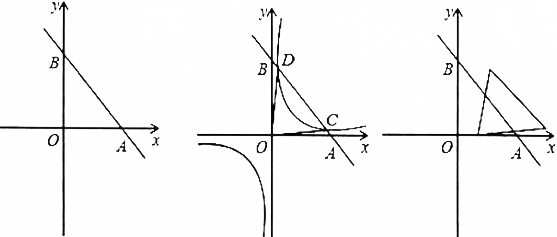
如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).
(1) m为何值时,△OAB面积最大? 最大值是多少?
(2)如图2,在(1)的条件下,函数y=k/x(k>0)的图像与直线AB相交于C,D两点,若S△OCA=1/8 S△OCD,求k的值.
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).

(1)∵A(m,0),B(0,n),∴OA=m,OB=n,S△AOB=mn/2,∵m+n=20,∴S△AOB=m(20-m)/2=-1/2 m²+10m=-1/2 (m-10)²+50∴当m=10时,S最大=50.(2)∵m=10,m+n=20∴n=10,∴A(10,0),B(0,10),设AB的解析式为y=kx+b,由图像得,解得∴y=-x+10.∵S△OCA=1/8 S△OCD,∴设S△OCD=8a,则S△OAC=a,∴S△OBD=S△OAC=a,∴S_(△AOB)=10a=50,∴S△AOC=a=5,∴1/2...
查看完整答案在平面直角坐标系xOy中,若反比例函数y=k/x(k≠0)的图像经过点A(1,2)和点B(-1,m),则m的值为______.
若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=8/x的图像上,则x1,x2,x3的大小关系是【 】
根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(㎡)的反比例函数,其函数图象如图所示,当S=0.25㎡时,该物体承受的压强p的值为______Pa.
若反比例函数y=k/x(k≠0)的图像经过点(2,-3),则它的图像也一定经过的点是【 】
在平面直角坐标系xOy中,若点A(2,y1),B(5,y2)在反比例函数y=k/x(k>0)的图像上,则y1 _____ y2(填“>”“=”或“<”).
如图,在Rt△ABC中,∠ABC=90°,C(0,-3),CD=3AD,点A在反比例函数y=k/x图像上,且y轴平分∠ACB.求k=________.
已知点A(x1,y1 ),B(x2,y2 ),C(x3,y3 )都在反比例函数y=k/x (k<0)的图像上,且x1<x2<0<x3,则y1,y2,y3的大小关系是【】