如图，在四边形ABCD中，AB//CD，AB≠CD，∠ABC=90°，点EF分别在线段BC、AD上，且EF//CD，AB=AF，CD=DE.
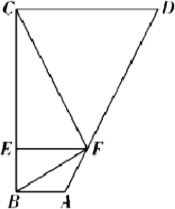
(1)求证：CF⊥FB;
(2)求证：以AD为直径的圆与BC相切;
(3)若EF=2，∠DFE=120°，求△ADE的面积.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2021年广东省）
答案解析
(1)∵CD=DF∴可设∠DCF=∠DFC=α则∠FDC=180°-2α∵CD//AB∴∠BAF=180°-(180°-2α)=2α,又∵AB=AF,∴∠ABF=∠AFB=(180°-2α)/2=90°-α,∴∠CFB=180°-∠CFD-∠BFA=180°-α-(90°-α)=90°∴CF⊥BF.(2)如图，取AD中点O，过O作OM⊥BC,∵AB//CD,∠ABC=90°∴∠DCB=90°,又∵OM⊥BC，∴OM//BC,∴M为BC的中点，∴OM=1/2(AB+CD).∴AD=AF+DF=AB+CD=2OM又∵OM⊥BC∴以AD为直径的圆与BC相切.(3)∵EF//CD∴ ...
查看完整答案