中考2015年广东省广州市( )
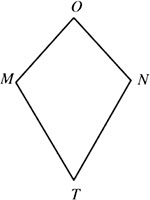
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8.
①是否存在一个圆使得 A、B、C、D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;
②)过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形 ABED为菱形时,求点F到 AB 的距离.
解答过程见word版
中考2015年广东省广州市( )
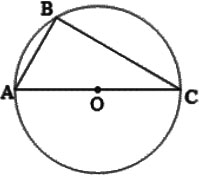
如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹不写作法);
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
解答过程见word版
中考2015年广东省广州市( )
如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF.求证:BE=AF.
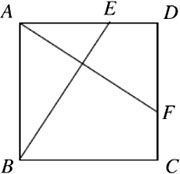
在正方形ABCD中,AB=AD,∠BAE=∠D=90°.
在△ABE和△ADF中,AB=AD,∠BAE=∠D,AE=DF.
∴△ABE≌△ADF(SAS),
∴BE=AF.
中考2015年广东省广州市( )
如图,四边形ABCD中,∠A=90°,AB=3√3,点M,N分别线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点 ,则EF长度的最大值为______.
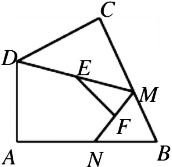
3
∵ED=EM,FM=FN,
∴EF=1/2 DN,
故,当DN最大时,EF最大.
∵N与B重合时,DN最大,此时DN=DB=6,
∴EF的最大值为3.
中考2015年广东省广州市( )
如图,AB║CD,直线1分别与AB、CD相交,若∠1=50°,则∠2的度数为______.
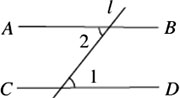
50°
两直线平等,内错角相等.

