考研2025年理工数学Ⅰ( )
投保人的损失事件发生时,保险公司的赔付额Y与投保人的损失额X的关系为
Y=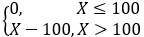
设损失事件发生时,投保人的损失额X的概率密度为
f(x)=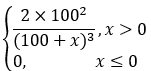
(1)求P{Y>0}及E(Y).
(2)这种损失事件在一年内发生的次数记为N,保险公司在一年内就这种损失事件产生的理赔次数记为M,假设N服从参数为8的泊松分布,在N=n(n≥1)的条件下,M服从二项分布B(n,P),其中P=P{Y>0},求M的概率分布.
解答过程见word版
考研2025年理工数学Ⅰ( )
设矩阵A=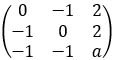 ,已知1是A的特征多项式的重根.
,已知1是A的特征多项式的重根.
(1)求a的值;
(2)求所有满足Aα=α+β,A²α=α+2β的非零列向量α,β.
解答过程见word版
考研2025年理工数学Ⅰ( )
设Σ是由直线 绕直线 (t为参数)旋转一周得到的曲面,Σ1是Σ介于平面x+y+z=0与x+y+z=1之间部分的外侧,
计算曲面积分∬Σ1xdydz+(y+1)dzdx+(z+2)dxdy.
解答过程见word版
考研2025年理工数学Ⅰ( )
设函数f(x)在区间(a,b)内可导,证明:导函数f'(x)在(a,b)内严格单调增加的充分必要条件是:对(a,b)内任意的x1,x2,x3,当x1<x2<x3时,(f(x2 )-f(x1))/(x2-x1 )<(f(x3 )-f(x2))/(x3-x2 )
解答过程见word版
考研2025年理工数学Ⅰ( )
已知函数f(u)在(0,+∞)内具有二阶导数,记g(x,y)=f(x/y),若g(x,y)满足:x²(∂²g)/(∂x² )+xy (∂²g)/∂x∂y+y²(∂²g)/(∂y² )=1,且g(x,x)=1, ∂g/∂x|(x,x)=2/x,求f(u).
解答过程见word版

