已知函数f(u)在(0,+∞)内具有二阶导数，记g(x,y)=f(x/y)，若g(x,y)满足：x²(∂²g)/(∂x² )+xy (∂²g)/∂x∂y+y²(∂²g)/(∂y² )=1，且g(x,x)=1, ∂g/∂x|_(x,x)=2/x，求f(u).

已知函数v(x,y,z)=xy²z³，向量n^→=(2,2,-1)，则 ∂v/(∂n)|_(1,1,1)=______.

求二元函数f(x,y)=x²(2+y²)+ylny的极值.

设二元函数f(x,y)在(x₀,y₀)的某邻域U内有定义，且在U内存在偏导数.

证明：若偏导数f_x(x,y)和f_y(x,y)都在(x₀,y₀)可微，则f_xy (x₀,y₀ )=f_yx (x₀,y₀).

若f(x)=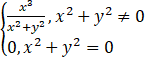，求在(0,0)处(cosα,sinα)'的方向导数为________.