已知函数f(x)=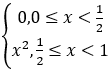的傅里叶级数为b_n sinnπx,S(x)为b_n sinnπx的和函数，则S(-7/2)=______.

已知级数①sin⁡(n³ π)/(n²+1) ，②(-1)ⁿ(1/∛n² -tan⁡1/∛n²) ，则【 】

A、①与②均条件收敛

B、①条件收敛，②绝对收敛

C、①绝对收敛，②条件收敛

D、①与②均绝对收敛

设函数f(x)连续可导，且f(0)=1,0<f'(x)<1/2.设{x_n}满足：x_n+1=f(n),(n=1,2,⋯)，证明：

(1)级数(x_n+1-x_n)绝对收敛.

(2)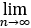x_n存在，且0<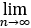x_n <2.

证明：函数项级数(-1)ⁿ/(x²+n)在区间x∈(-∞,+∞)上一致收敛.

求幂级数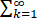(-1)^n-1/(2n-1) x²ⁿ的收敛域及和函数.