考研2025年理工数学Ⅰ( )
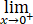 (xx-1)/(lnx∙ln(1-x))=______.
(xx-1)/(lnx∙ln(1-x))=______.
-1
解答过程见word版
考研2024年北京邮电大学( )
设函数f(x)在区间[0,+∞)上可微,且满足条件:
0≤f(x)≤x/(1+x²)(0≤x<+∞)
求证:存在ξ>0,使得f'(ξ)=(1-ξ²)/(1+ξ²)².
解答过程见word版
考研2024年北京邮电大学( )
讨论:当α>0时,函数f(x)=xα在区间[0,+∞)上的一致连续性.
解答过程见word版
考研2024年北京邮电大学( )
当x→0时,xe-x/2与αxn是等价无穷小,求α和n.
解答过程见word版
考研2024年北京邮电大学( )
证明:若an>0,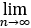 an/an+1 =l>1,则
an/an+1 =l>1,则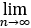 an=0.
an=0.
解答过程见word版

