已知z=z(x,y)由z+lnz-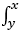
xe-t² dt=1确定，则∂²z/∂x²|(1,1)=______.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
微分方程xy'-y+x²ex=0满足条件y(1)=-e的解为y=________.
设g(x)是函数f(x)=1/2 ln(3+x)/(3-x)的反函数，则曲线y=g(x)的渐近线方程为__________.
总体X的均匀分布为F(X),X1,X2,⋯,Xn为来自总体X的简单随机样本，样本的经验分布函数为Fn(x)，对于给定的x(0<F(x)<1),D(F(x))=【 】
设随机变量X服从正态分布N(-1,1),Y服从正态分布N(1,2)，若X与X+2Y不相关，则X与X-Y的相关系数为【 】
设矩阵A= ,B=，若f(x,y)=|xA+yB|是正定二次型，则a的取值范围是【 】
设A为3阶矩阵，则“A³-A²可对角化”是“A可对角化”的【 】
已知A是m×n矩阵，β是m维非零向量.若A有k阶非零子式，则【 】
设函数f(x)连续，则∫01dy ∫0yf(x) dx【 】
设函数f(x,y)=ext²dt，则∂²f/∂x∂y|(1,1)=______
设u=u(x,y,z),v=v(x,y,z),w=w(x,y,z)由x=u+v+w,y=uv+uw+vw,z=uvw确定，求∂u/∂x,∂u/∂y,∂u/∂z.
设函数f(u,v)具有2阶连续偏导数，且df|(1,1)=3du+4dv，令y=f(cosx,1+x²)，则d²y/dx²|x=0=______.
若f(x)=|x|α，求(∂² f)/(∂x1² )+(∂² f)/(∂x2² )+(∂² f)/(∂x3² )+⋯+(∂² f)/(∂xn² )=________.
设二元函数f(x,y)在(x0,y0)的某邻域U内有定义，且在U内存在偏导数.证明：若偏导数fx(x,y)和fy(x,y)都在(x0,y0)可微，则fxy (x0,y0 )=fyx (x0,y0).
设函数z=z(x,y)由z+lnz-∫yxe-t² dt=0确定，则∂z/∂x+∂z/∂y=【 】
设φ(t),ψ(t)有二阶连续导数，u=φ(y/x)+xψ(y/x)，求：x2 ∂2u/∂x2+2xy ∂2u)/∂x∂y+y2 ∂2u/∂y2.