设矩阵A=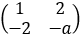 ,B=
,B=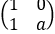 ,若f(x,y)=|xA+yB|是正定二次型,则a的取值范围是【 】
,若f(x,y)=|xA+yB|是正定二次型,则a的取值范围是【 】
A、(0,2-√3)
B、(2-√3,2+√3)
C、(2+√3,4)
D、(0,4)
设矩阵A=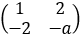 ,B=
,B=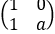 ,若f(x,y)=|xA+yB|是正定二次型,则a的取值范围是【 】
,若f(x,y)=|xA+yB|是正定二次型,则a的取值范围是【 】
A、(0,2-√3)
B、(2-√3,2+√3)
C、(2+√3,4)
D、(0,4)
B
【解析】
解答过程见word版
已知矩阵A=与B=合同.(1) 求a的值及k的取值范围;(2) 若存在正交矩阵Q,使得QTAQ=B,求k及Q.
设A=为n×n正定矩阵,证明:|A|≤a11 a22…ann.其中符号|∙|表示行列式.
设A是n阶正定矩阵,B为n阶实方阵,证明:(1)若B'=B,则AB的特征值为实数;(2)若B正定,则AB的特征值皆大于0;(3)若B正定,且AB=BA,则AB正定。
设A,B均为n阶实对称阵,A的特征值均小于a,B的特征值均小于b.证明:对任意的k>a+b,A+B-kE是负定矩阵.
设A是n阶正定矩阵,E是n阶单位矩阵,证明A+E的行列式大于1.
设A是n级实对称矩阵,证明rank(A)=n的充要条件是:存在实对称矩阵B使AB+B'A是正定矩阵。
设S1,S3为实对称矩阵,S2为实矩阵,则矩阵S=为正定矩阵的充要条件为矩阵S3与矩阵S1-S2 S3-1 S2'皆为正定矩阵。
设函数f(x)=(1+x)/(1+nx2n),则f(x)【 】
设二次型f(x1,x2,x3 )=xT Ax在正交变换下可化成y1²-2y2²+3y3²,则二次型f的矩阵A的行列式值与迹分别为【 】
设矩阵A=,Mij表示A的i行j列元素的余子式.若|A|=-1/2,且-M21+M22-M23=0,则【 】
设随机变量X的概率密度为f(x)=,则X的三阶中心矩E(X-EX)³=【 】
随机变量X,Y相互独立,其X~N(0,2),Y~N(-1,1),记p1={2X>Y},p2={X-2Y>1},则【 】
二次型f(x1,x2,x3 )=x1²+2x1 x2+2x2 x3的正惯性指数为【 】
已知矩阵A=的特征值λ对应的特征向量α=,求该矩阵的若当(Jordan)标准型.
设实矩阵A=(1)求A的若尔当标准形J.(2)求可逆矩阵P,使得P-1AP=J.
已知二次型f(x1,x2,x3 )=3x12+4x22+3x32+2x1 x3,(1)求正交变换x=Qy将f(x1,x2,x3)化为标准形;(2)证明minx≠0f(x)/(xT x)=2.
二次型f(x1,x2,x3 )=(x1+x2 )2+(x1+x3 )2-4(x2-x3 )2的规范型为【 】
二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【 】
求一个正交变换,化二次型f=x12+4x22+4x32-4x1 x2+4x1 x3-8x2 x3成标准形.
已知二次型f(x1,x2,x3 )=2x12+3x22++3x32+2ax2 x3 (a>0)通过正交变换化成标准形f=y12+2y22+5y32,求参数a及所用的正交变换矩阵.