初中数学-中考试题(天津市 2022年三角函数)

问答题（2022年天津市）

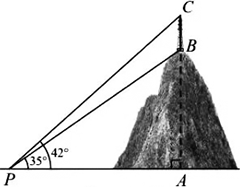
如图，某座山AB的顶部有一座通讯塔BC，且点A,B,C在同一条直线上，从地面P处测得塔顶C的仰角为42°，测得塔底B的仰角为35°.已知通讯塔BC的高度为32m，求这座山AB的高度(结果取整数).

参考数据：tan35°≈0.70，tan42°≈0.90.

答案解析

如图，根据题意，BC=32,∠APC=42°,∠APB=35°.在Rt△PAC中，tan∠APC=AC/PA⟹PA=AC/(tan∠APC).在Rt△PAB中，tan∠APB=AB/PA⟹PA=AB/(tan∠APB).∵AC=AB+BC,∴(AB+BC)/(t...

查看完整答案

讨论

三角函数

如图，已知在Rt△ABC中，∠ACB=90°,AC=1,AB=2,则sinB的值是______.

计算|1-tan60°|的值为【】

tan45°的值等于【】

某兴趣小组借助无人飞机航拍校园如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°.已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度.(结果保留根号)

假设小丽的眼睛距地面1.5米，当她站在C点时，测出旗杆A的仰角为 30°，如果向前走 10米到达点E，此时的仰角为60°，求旗杆AB的高度.

如图，学校环保社成员想测量斜坡 CD 旁一棵树AB 的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为20m，DE的长为10cm，则树AB的高度是【】m.

方程x2+4x+3=0的两个根为【】

已知抛物线y=ax2+bx+c，（a,b,c是常数，0<a<c）经过点(1,0)，有下列结论：① 2a+b<0；② 当x>1时，y随x的增大而增大；③ 关于x的方程ax2+bx+(b+c)=0有两个不相等的实数根.其中，正确的个数是【】

不透明袋子中装有9个球，其中有7个绿球、2个白球，这些球除颜色外无其它差别.从袋子中随机取出1个球，则它是绿球的概率是________.

tan45°的值等于【】

三角形

如图，已知点O是△ABC的外心，∠A=40°，连结BO、CO则∠BOC的度数是【】

如图，在△ABC中，点D、E分别是BC、AC的中点，AD与BE相交于点F，若BF=6，则BE的长是________.

我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a,b,c，记p=(a+b+c)/2，则其面积S=.这个公式也被称为海伦-秦九韶公式.若p=5,c=4，则此三角形面积的最大值为【】

以下虚线框中为一个合作学习小组在一次数学实验中的过程记录，请阅读后完成虚线框下方的问题1~4.(1)在Rt△ABC中，∠C=90°,AB=2，在探究三边关系时，通过画图，度量和计算，收集到，组数据如下表:(单位:厘米)(2)根据学习函数的经验，选取上表中BC和AC+BC的数据进行分析；①设BC=x,AC+BC=y，以(x,y)为坐标，在图①所示的坐标系中描出对应的点；②连线；观察思考(3)结合表中的数据以及所面的图像，猜想.当x=__________时，y最大；(4)进一步C猜想:若Rt△MBC中，∠C=90°，斜边AB=2a(a为常数，a>0)，则BC= _________时，AC+BC最大.推理证明(5)对(4)中的猜想进行证明.问题1.在图①中完善(2)的描点过程，并依次连线；问题2.补全观察思考中的两个猜想:(3) _______ (4) _______问题3.证明上述(5)中的猜想:问题4.图②中折线B-E-F-G-A是一个感光元件的截面设计草图，其中点A,B间的距离是4厘米，AG=BE=1厘米，∠E=∠F=∠G=90°,平行光线从AB区域射入，∠BNE=60°,线段FM、FN为感光区城，当EF的长度为多少时，感光区域长度之和最大，并求出最大值.

如图，四边形ABCD是矩形，延长DA到点E，使AE=DA，连接EB，点F1是CD的中点，连接EF1，BF1，得到ΔEF1B；点F2是CF_1的中点，连接EF2，BF2，得到ΔEF2 B；点F3是CF2的中点，连接EF3，BF3，得到ΔEF3 B；…；按照此规律继续进行下去，若矩形ABCD的面积等于2，则ΔEFn B的面积为_________.（用含正整数n的式子表示）

如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝6，AC＝5，则△ACE的周长为【】

已知△ABC的三个顶点都是同一个正方形的顶点，∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为6，则点D到直线AB的距离为________.(结果要化简，不能含三角函数)

在ΔABC中，∠ABC=90°，AB=2，BC=3，点D为平面上一个动点，∠ADB=45°，则线段CD长度的最小值为________.

如图，在Rt△ABC中，∠A=90°，作BC的垂直平分线交AC于点D，延长AC至点E，使CE=AB. (1)若AE=1，求△ABD的周长;(2)若AD=1/3 BD，求tan∠ABC的值.

如图，边长为1的正方形ABCD中，点E为AD的中点，连接BE，将ABE沿BE折叠得到△FBE，BF交AC于点G，求CG的长.

坐标系与函数

如图，一次函数y=kx+b 与反比例函数y=m/x(x>0)交于A(2,4),B(a,1)，与x轴，y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=m/x(x>0)的表达式；(2)求证：AD=BC.

二次函数y=ax²+bx+c(a≠0)的图像如图所示，下列结论正确提【】

已知顶点为A的抛物线y=a(x-1/2)²-2经过点B(-3/2,2)，点C(5/2,2).(1)求抛物线的解析式；(2)如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠0PM=∠MAF，求△POE的面积；(3)如图2，点Q是折线A-B-C上一点，过点Q作QN//y 轴，过点E作EN//x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标.

已知y=ax²+bx+c(a≠0)的图像如图，则y=ax+b和y=c/x的图像为【】

已知点A(x1,y1 )，B(x2,y2 )，C(x3,y3 )都在反比例函数y=k/x (k<0)的图像上，且x1<x2<0<x3，则y1，y2，y3的大小关系是【】

竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0表示，其中h0 (m)是物体抛出时离地面的高度，v0 (m/s)是物体抛出时的速度．某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出，小球达到的离地面的最大高度为【】

若函数y=ax2+bx+c(a≠0)的图象如图所示，则函数y=ax+b和y=c/x在同一平面直角坐标系中的图象大致是【】

如图所示，抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点，与y轴交于点C，且点A的坐标为A(-2,0)，点C的坐标为C(0,6)，对称轴为直线x=1.点D是抛物线上一个动点，设点D的横坐标为m(1<m<4)，连接AC，BC，DC，DB. （1）求抛物线的函数表达式；（2）当ΔBCD的面积等于ΔAOC的面积的3/4时，求m的值；（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B,D,M,N为顶点的四边形是平行四边形.若存在，请直接写出点M的坐标；若不存在，请说明理由.

如图，在平面直角坐标系中，抛物线y=ax2+bx-2交x轴于A，B两点，交y轴于点C，且OA=2OC=8OB.点P是第三象限内抛物线上的一动点. （1）求此抛物线的表达式；（2）若PC//AB，求点P的坐标；（3）连接AC，求ΔPAC面积的最大值及此时点P的坐标.

把函数y=(x-1)2+2的图象向右平移1个单位长度，平移后图象的函数解析式为【】