设函数f(x)在x=0处连续,且
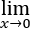 (xf(x)-e2sinx+1)/(ln(1+x)+ln(1-x))=-3
(xf(x)-e2sinx+1)/(ln(1+x)+ln(1-x))=-3
证明:f(x)在x=0处可导,并求f'(0).
设函数f(x)在x=0处连续,且
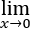 (xf(x)-e2sinx+1)/(ln(1+x)+ln(1-x))=-3
(xf(x)-e2sinx+1)/(ln(1+x)+ln(1-x))=-3
证明:f(x)在x=0处可导,并求f'(0).
解答过程见word版
设函数f(x)在区间(-1,1)内有定义,且f(x)=0,则【 】
设函数f(x)在区间(-1,1)上有定义,且f(x)=0,则【 】
证明:(f(x0+h)-f(x0-k))/(k+h)存在的充要条件为f在x0处可导.
设f(x)在x=a的某个领域内有定义,则f(x)在x=a处可导的一个充分条件是【 】
函数f(x)=(x2-x-2)|x3-x|不可导点的个数是【 】
设f(x)=其中g(x)是有界函数,则f(x)在x=0处【 】
已知函数f(x)在x=1处可导且(f()-3f(1+sin2x))/x2 =2,求f'(1).
设函数f(x)在(-∞,+∞)内有定义,对任意x都有f(x+1)=2f(x),且当0≤x≤1时f(x)=x(1-x2),试判断在x=0处函数f(x)是否可导.