已知函数f(x)=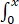 et²sintdt,g(x)=
et²sintdt,g(x)=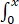 et²dt∙sin²x,则【 】
et²dt∙sin²x,则【 】
A、x=0是f(x)的极值点,也是g(x)的极值点
B、x=0是f(x)的极值点,(0,0)是曲线y=g(x)的拐点
C、(0,0)是y=f(x)的拐点,x=0是g(x)的极值点
D、(0,0)是曲线y=f(x)的拐点,也是曲线y=g(x)的拐点
已知函数f(x)=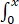 et²sintdt,g(x)=
et²sintdt,g(x)=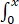 et²dt∙sin²x,则【 】
et²dt∙sin²x,则【 】
A、x=0是f(x)的极值点,也是g(x)的极值点
B、x=0是f(x)的极值点,(0,0)是曲线y=g(x)的拐点
C、(0,0)是y=f(x)的拐点,x=0是g(x)的极值点
D、(0,0)是曲线y=f(x)的拐点,也是曲线y=g(x)的拐点
B
【解析】
解答过程见word版
已知函数f(x)=∫0xet² sintdt,g(x)=∫0xet²dt∙sin²x,则【 】
曲线y=(t-1)(t-2)dt在点(0,0)处的切线方程是____________.
设f(x)有二阶连续导数,且f' (0)=0,f''(x)/|x|=1,则【 】
确定函数y=(x+1)/x2 的单调区间、极值、凸凹区间、拐点以及渐近线.
设在区间[a,b]上f(x)>0,f' (x)<0,f''(x)>0,记S1=f(x)dx,S2=f(b)(b-a),S3=1/2[f(a)+f(b)](b-a),则【 】
设函数f:[0,1]→R是连续的且在(0,1)上可微,若f满足:(1) f(0)=0;(2)存在常数M>0使得|f'(x)|≤M|f(x)|对任意x∈(0,1)成立.证明:在[0,1]上f(x)=0.
曲线y²=x在点(0,0)处的曲率圆方程为____________________.
函数f(x,y)=2x³-9x²-6y4+12x+24y的极值点是__________.
某产品的价格函数为p=,(p为单价,单位:万元;Q为产量,单位:件),总成本函数为C=150+5Q+0.25Q²(万元),则经营该产品可获得的最大利润为______(万元).
已知方程a1/(x-λ1 )+a2/(x-λ2 )+a3/(x-λ3 )=0其中a1,a2,a3>0,λ1<λ2<λ3.证明:此方程在区间(λ1,λ2)和(λ2,λ3)中各有一根.
设f(x)=(x-x0 )n φ(x),其中n为正整数,φ(x)在x0连续且φ(x0 )≠0,讨论f(x)在x0处能否取极值?