解 答 题(数学·2025年·广东省广州市)
某玩转数学小组发现隧道前通常设有涉水线和限高架等安全警示,为探究其内在的数学原理,该小组考察了如图1所示的双向通行隧道.以下为该小组研究报告的部分记录,请认真阅读,解决问题.

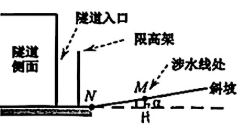
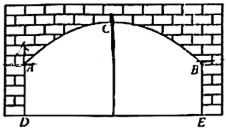
图1 图2 图3
(一)、涉水线设置
1、数学抽象绘制图形:隧道及斜坡的侧面示意图可近似如图 2所示.
2、信息收集资料整理:当隧道内积水的水深为0.27 米时(即积水达到涉水线处),车辆应避免通行.
3、实地考察数据采集:斜坡的坡角α为10°,并查得
sin10°≈0.174,cos10°≈0.985,tan10°≈0.176.
(二)、限高架设置
1、数学抽象绘制图形:图3为隧道横截面示意图,由抛物线的一部分ABC和矩形ADEB的三边构成.
2、信息收集资料整理:车辆进入隧道,应在行驶车道内通行(禁止压线),且必须保证车辆顶部与隧道顶部ABC在竖直方向的空隙不小于0.3米.
3、实地考察数据采集:隧道的最高点C到地面DE距离为5.4米,两侧墙面高AD=BE=3米,地面跨度DE=10米,车辆行驶方向的右侧车道线(宽度忽略不计)与墙面的距离为1米.
问题解决:
⑴如图2,求涉水线离坡底的距离M(精确到0.01米);
⑵在图3中建立适当的平面直角坐标系,求抛物线ABC的解析式;
⑶限高架上标有警示语“车辆限高h米”(即最大安全限高),求h的值(精确到0.1 米).
解答提示
解答过程见word版
自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是【 】
下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是【 】
泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】
如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积24cm2是的有盖的长方体铁盒.则剪去的正方形的边长为cm.
如图,在RtΔABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为.
如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC于点F,求∠C和∠E的度数.

